تدوين متجه الوحدة | المتجهات والفراغات | الجبر الخطي | أكاديمية خان
عندما يشرحون البعد W ، يتم تمثيله على أنه الجانب السلبي من المحور X. لماذا البعد W سالب X؟ أليس حقا هو البعد الخاص؟

- حاول رسم رسم بياني رباعي الأبعاد على سطح ثنائي الأبعاد. هذا ما توصلوا إليه (حقك على الرغم من أنه ليس رسمًا بيانيًا رائعًا).
كما ذكرNendoTaka ، من الصعب جدًا رسم كائن رباعي الأبعاد على سطح ثنائي الأبعاد.
إليك كيفية عمل الأبعاد:
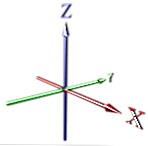
مع بُعد واحد ، يتم إرسال نقطة بلا حدود ، مما يؤدي إلى إنشاء خط (انظر X)
في 2d ، نضيف بعدًا عموديًا على ذلك (انظر X ، Y).
ثم نذهب بشكل عمودي مرة أخرى ونتوسع لأعلى لنحصل على البعد الثالث (انظر X ، Y ، Z).
نظرًا لأن ثلاثي الأبعاد> ثنائي الأبعاد ، لا يمكننا تمثيل ذلك جيدًا على الورق دون طي الورق أو إضافة المزيد من الأوراق فوقه - وكل ذلك غير عملي حقًا للعرض على الشاشة. لذلك ، بدلاً من ذلك ، نستخدم المنظور - كيف ترى أعيننا ثلاثية الأبعاد. عادة الزوايا هنا ~ 30 درجة.

وهذا يبدو جيدًا ، لأن أعيننا لا ترى بالمعنى التقليدي ثلاثي الأبعاد ، لذا فإن محاكاة ذلك يعمل. لكن عندما نريد تمثيل البعد الرابع ، فليس لدينا ما نقارن به. نحتاج إلى العودة إلى الوضع العمودي مرة أخرى وهذا أمر يصعب على أعيننا فهمه نظرًا لعدم وجود الكثير من المراجع.
فيما يلي مثال على تصوير البعد الرابع:
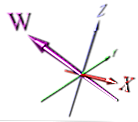
هذه طريقة أكثر صحة لعرض البعد ، لكنها لا تزال تعتمد على المنظور - كما أنه ليس من الواضح على الفور أنه بُعد جديد للوهلة الأولى.
ربما اختار رسامو الرسوم المتحركة القيام بشيء بسيط يكون من الأسهل تحريكه. على الرغم من أنك إذا قمت بتدوير الصورة أعلاه ، فقد يتداخل الأبعاد X و W - وهذا لن يكون واضحًا في الصورة بدون مؤشرات الأسهم.
حسنًا ، إنهم مخطئون - ولكن لا توجد أيضًا طريقة بسيطة لتمثيل 4 أبعاد على ورقة واحدة
تنسيق مصادر الصور وقراءة جيدة
3- 1 لكي نكون منصفين ، هناك العديد من الطرق القياسية لإسقاط كائنات رباعية الأبعاد مثل القطع الصغيرة والأشكال الثلاثية في 3 أبعاد (ثم إلى بعدين بالطرق المعتادة) والتي تفوق كثيرًا تلك المستخدمة في العرض ، منها ميزة إضافية تتمثل في المظهر الأكثر برودة من تلك المستخدمة في العرض.
- senshin أوه بالتأكيد ، لكني أعتقد أن رسامي الرسوم المتحركة أرادوا أيضًا شرح شيء ما ، بدلاً من الدهشة
- 1 يمكنك استخدام أشياء أخرى غير الموضع للإشارة إلى مدى طول المحور ، مثل اللون.